This post is part of the SATF work.
One particular testing issue requires some special measures, but could also be addressed within the approach proposed in the “Solution” section. The issue is testing of the nondeterministic aspects of robotics systems, which are inherent and abundant within the field. If the outcome of a given test is nondeterministic i.e., every single run of the test, the initial configuration being the same, could end up with either a failure or a success, then neither of them would imply the definitive answer to the real question behind the test – an attempt to assess some nondeterministic process. There are two distinctive flavours of this problem.
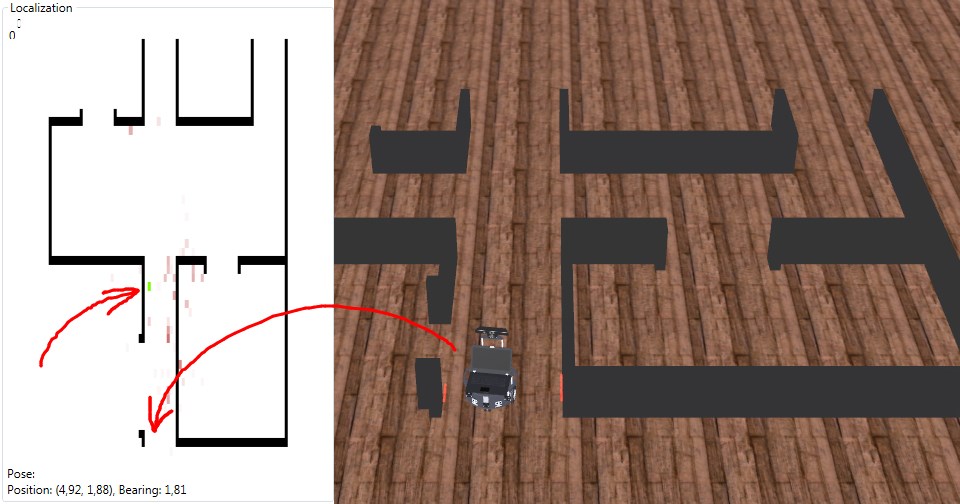
The first is testing of the nondeterministic algorithms. These algorithms not only produce different results for different runs with the same initial state, but they could even fail occasionally. Let’s take the Monte Carlo localization algorithm in the global localization mode as an example. In the pure MC localization (without special measures intended to mitigate the very described effect) at the beginning of the algorithm, the entire map is randomly and uniformly populated with a fixed number of position samples. The fittest of which will survive during the next measurement-update steps to represent the most likely robot position hypotheses. There exists a non null probability that no samples in the vicinity of the real robot position are generated at the initial step. Thus failing the whole localization algorithm. But a single fail like this does not vindicate an error in the algorithm’s implementation. In that case, the test success criterion can be stated as a condition on the probability of successful localization (where random is the algorithm).
In the second case, nondeterministic is the environment, not the algorithm. And the test criterion could also be stated as a condition on the success probability (where random is the environment). For example, let’s consider a vehicle driving across a passable cross country terrain, and the goal is to test its stability. The vehicle can happen to topple on any concrete terrain. And we can impose a boundary on the maximum value of the toppling probability as a requirement. Meaning that for every terrain of a given type, the probability of vehicle toppling should be no more than some required threshold. Here, random is the cross country terrain.
 Vehicle upon cross country terrain
Vehicle upon cross country terrain
In both cases, the test success criterion is not the result of a single test run but the probability of its success. The only way to lay hands on that value is to approximate it as a frequency of successes over a series of test runs. Applying the central limit theorem (provided test runs are independent), varying a number of runs and taking into account the criterion probability value, a reasonably stable test behavior could be achieved. The principal difference between the two problem flavours above is the locus of uncertainty: inside or outside of the robot’s software. In former case, randomness is embedded into the software under test, so the testing framework has nothing to do but rerun the same test multiple times. The latter case demands randomness on the part of environment, thus there should be a way to introduce artificial probabilistic noise into the simulation on each test run. In the example above, it could be made either via random terrain regeneration, or just via placing the vehicle in a random location with a random bearing on the same terrain.
Essentially, the approach to testing of nondeterministic issues reduces to multiple rerunning of the tests in order to assess not only single test run’s result, but its success rate. Now that I have finished the section, I am not absolutely certain if I have succeeded in conveying its message. That’s why “One particular testing issue requires some special measures…”
| Previous | Next |